I have been JZOI for ten days!

可以说,纪念中学的生活是枯燥的。每天有充裕的时间来教室,也有充裕的时间可以偷偷腐slayone。正因为如此,每一个人才会去快一点改题,然后超越别人。
感觉来说,跟三鑫的生活”文化课”差不多。每天早晨都有考试,下午讲题+改题,晚上改题 or 讲知识点。

不过,还是学到了很多道理、方法和知识的。比如tarjan,zkw费用流,看了看树套树,看了看AC自动机和后缀数组排序,学会如何使用主席树,贪心的正确性,Bfs爆搜形式,hash的血腥惨案…..同时,在考试中,我们要先用30分钟来看题,确定难度,可做性,顺带想一想思路。然后用大约60分钟的时间想,并且做一道题。虽然本人太蒟蒻,没有几次好成绩,不过这种方法用在考试的时候特别爽。

其次,JZOI的学习气氛是值得体验的。以前我是来过的(小学),不过后来又被淘汰了。现在重新回到JZOI,感觉很轻盈,又很沉重,所以需要加大努力。

So manty story

I.phone的限制

JZ这种高校肯定是限制手机的。有一天我们教练进来,说如果谁带了手机,上交,不然被发现或者被举报了就直接退队。当时很吓人,鸦雀无声,因为很多人都带了。然后我们有一部分怂了一下,就交了,然后度过了愉快的10天。DH大佬就是最不怂的人之一,在宿舍里说:”你们这些人怂什么,只要你不在宿管面前浪就可以了”,赢得我们一致的支持。不过5分钟,宿管破门而入,盯住DH大佬的手机那微弱的光,然后穿进床上抓过手机,就走了。我们还没有反应过来DH就出去了。正所谓任何物体不能达到光速,所以这也是一个亚光速打脸了。

还有一次,GSM大佬正在听着歌玩手机,我就出去了,宿管和我擦肩而过。我走了大概5步,突然转身回跑,发现已经没得救了,所以就跑走了。晚上回来,GSM大佬的手机没有被收,我问您是如何做到的,他说他对宿管做了一个ok的手势。

II.World cup 乱入的OI

得知要去JZOI的那天,德国输了。进入JZ的前一个晚上,阿根廷输了。写这篇文章的前几天,英格兰炸了,接着又炸了一次。每天我们都可以用手机看世界杯。昨天就看了决赛,网上大喊fu(此字母自行脑补)k国进球!克罗地亚干嘛干嘛。全宿舍可能就只有一位大佬YSJ支持克罗地亚。有人支持姆巴佩,有人支持乌姆蒂蒂….所以YSJ也是身份尴尬。晚上我的手机出现4种形态:我们用线段树来表示:

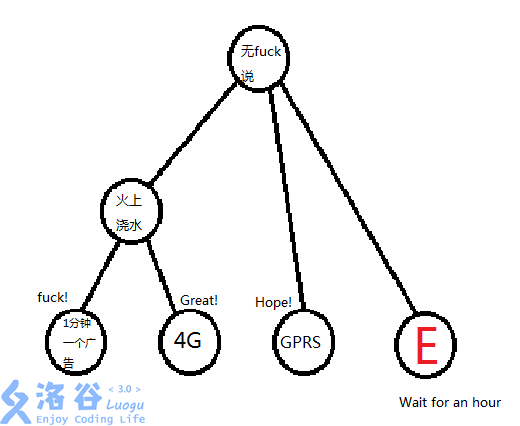
Picture

然后我就没看到一些细节。

旁边的C组大佬玩狼人杀到12点我也是醉了,还不如去看鬼片。

III.How was the food?

一定要记住,5元的菜华而不实,6元的菜稀有难见,3元的菜吃不饱,只有3.5,4元的才是最经济且最好的!!!!!!
(注明:1.5的通心菜量最多,3.5元的肉末豆腐吃的最快最实惠,4元酱香鸡是最好吃的,吃完饭禁忌喝任何小卖部饮料,不然你就会变成望庐山瀑布)

好吧,其实豆腐的能量很多,建议吃士力架。

Come back about OI

学了些什么?我不是讲了吗?
不过发现我会很多东西,比如主席树,最大流/费用流,哈密尔,割点都是很多人不会的,不过就是没有考什么好分数,所以一直属于颓废状态。

然后说一下生活细节:
早上起来大叫一声fu(此字母自行脑补)k,然后快速刷牙。JZOI的厕所是肮脏而不失凌乱的,还有里面神秘而不是优雅的气味让人永生难忘。所以我们练就了一身的快速刷牙,快速洗澡,快速上厕所,一般都是O(1)实现的,像我这种蒟蒻可能就要O(log k)来实现了(k为常数)。去吃早餐,早餐有很多面包之类的,然我想起三鑫,所以就没有吃过面包——除了远近闻名的肠仔包以外。一般吃炒河粉,而且连续10天都如此。

早上考试,不是很喜欢打表,不过被生活压迫着,就不得不打表。有些时候还是会有好成绩的吧,我想,多考图论,少考DP,我就可以AK。不过并不然,我们的管理员ROOT一共A了将近3000道题,数量最高的是DP。所以我不得不在初二的时候努力加紧DP训练。

中午又去吃饭,经常回去小卖部卖东西吃。还有午休,一般我都会腐败。

下午教练就叫成绩最好的那一个人上来组织讲题,我也就只能弱弱的上那么2,3次,不过还是写了很多题解然后匿名上交的。然后改2个钟题目,爽死。

下午一放学,其余一部分人去打篮球、足球。我就先跑回宿舍洗澡,引用《阿长与山海经》的一句话,”一年的劫难总算完了”,我也想到是”一天的劫难总算完了”。洗完澡还有5分钟才开饭,所以就慢慢去饭堂,吃完直接就去教室,这是三鑫的好习惯——节约了2小时的时间!晚上改题,又是爽死。

半夜,夜话不断,宿管一夜破门3次以上,使得我们压制不住内心的骚动。但我还是坚持腐败。晚上10点左右回去,可以改题改到10:40。晚上可以去吃夜宵,有鸡肠,肉串,鸡扒什么之类的,很难想到JZ怎么强(虽然好几年前就吃过log(4)次)

ZJL大佬上了log k(都说了k为常数)次厕所后,我就入睡了,迎接下一天的考试。

Problem sets

下面的都是福利啊!!!!

7.06 排名:11/11

T1 矩阵

Description

N(2<=N<=500)个矩阵相乘，求进行乘法的最少次数，我们认为两个矩阵A(m*n)*B(n*p)的乘法次数为m*n*p次。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
Input

　　输入文件的第1行有两个正整数n和k，描述了圆环上的格子数与取数的范围。
　　第2行有n个正整数，按顺时针方向描述了圆环上每个格子上的数，且指针一开始指向了第1个数字所在的格子。
　　所有整数之间用一个空格隔开，且不超过10000。

Output

　　输出文件仅包括1个整数，为取完所有数的最小代价。

Sample Input

6 1
4 1 2 3 1 3

Sample Output

21

运用一些dp(类似于floyd)常识和矩阵乘法的原理。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
Uses math;

var
        n,i,j,k:longint;
        x,y:array[0..510] of longint;
        table:array[0..510,0..510] of longint;

begin
        read(n);
        for i:=1 to n do
                read(x[i],y[i]);
        for i:=1 to n do
                for j:=1 to n do
                        if i<>j then
                                table[i,j]:=maxlongint div 843;
        for j:=2 to n do
                for i:=j-1 downto 1 do
                        for k:=i to j-1 do
                                table[i,j]:=min(table[i,j],table[i,k]+table[k+1,j]+x[i]*y[k]*y[j]);
        writeln(table[1,n]);
end.

T2 圆环取数

Description

守护者拿出被划分为n个格子的一个圆环，每个格子上都有一个正整数，并且定义两个格子的距离为两个格子之间的格子数的最小值。环的圆心处固定了一个指针，一开始指向了圆环上的某一个格子，你可以取下指针所指的那个格子里的数以及与这个格子距离小于k的格子的数，取一个数的代价即这个数的值。指针是可以转动的，每次转动可以将指针由一个格子转向其相邻的格子，且代价为圆环上还剩下的数的最大值。现在对于给定的圆环和k，求将所有数取完所有数的最小代价。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
Input

　　输入文件的第1行有两个正整数n和k，描述了圆环上的格子数与取数的范围。
　　第2行有n个正整数，按顺时针方向描述了圆环上每个格子上的数，且指针一开始指向了第1个数字所在的格子。
　　所有整数之间用一个空格隔开，且不超过10000。

Output

　　输出文件仅包括1个整数，为取完所有数的最小代价。

Sample Input

6 1
4 1 2 3 1 3

Sample Output

21

发现是某一个oj的考试题,不多说,区间dp。有2个转移方程的,也有3个的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
Uses math;

var
        n,m,i,k,l,j,ans,add:longint;
        num:array[0..2100] of longint;
        maxn,table:array[0..2100,0..2100] of longint;

procedure Clean;
var
        i,j:longint;
begin
        for i:=0 to n do
                for j:=0 to n do
                        table[i,j]:=maxlongint div 843;
end;

procedure Max_number_make;
var
        i,j:longint;
begin
        for i:=1 to n do
                for j:=i+1 to n do
                begin
                        maxn[i,j]:=max(maxn[i,j-1],num[j]);
                        maxn[j,i]:=maxn[i,j];
                end;
end;

begin
        Clean;

        read(n,k);
        for i:=1 to n do
        begin
                read(num[i]);
                inc(add,num[i]);
                maxn[i,i]:=num[i];
                table[i,i]:=num[i];
        end;

        Max_number_make;

        if k*2+1>=n then
        begin
                writeln(add);
                exit;
        end;

        for l:=1 to n-2*k do
        begin
                for i:=k+2 to n-k-l do
                begin
                        j:=i+l;
                        table[i,j]:=min(table[i+1,j]+maxn[i,j],table[j-1,i]+(i+n-j-2*k-1)*maxn[i,j]);
                end;
                for i:=n-k downto k+2+l do
                begin
                        j:=i-l;
                        table[i,j]:=min(table[i-1,j]+maxn[i,j],table[j+1,i]+(j+n-i-2*k-1)*maxn[i,j]);
                end;
        end;

        writeln(max(table[k+2,n-k],table[n-k,k+2])+add);
end.

T3 扑克游戏

Description

有一棵无穷大的满二叉树，根为star，其余所有点的权值为点到根的距离，如图： 　　 　　现在你有一些扑克牌，点数从1到13，你要把这些扑克牌全部放到这个树上： 　　1. 当你把点数为i的扑克牌放在权值为j的点上，那么你会得到i*j的分数。 　　2. 当你把一个扑克牌放在一个节点上，那么你就不能把别的扑克牌放在这个节点以及这个节点的子树上。 　　你的目标是最小化你的得分。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
Input

　　文件名为 poker.in
　　输入第一行为一个数字N，表示你有的扑克牌数；
　　接下来一行N个数字，数字在1到13之间。

Output

　　文件名为 poker.out
　　一个数字，最小得分。

Sample Input

3
5 10 13

Sample Output

43

这题不是合并果子吗?

看了看HULLFMAN TREE,然后又不明白为什么当做合并果子。然后再熟练一下建模就可以了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
var
        heap:array[1..141000] of longint;
        i,j,n,m,ans,k:longint;

procedure down(x,n:longint);
var
        son:longint;
        t:longint;
begin
        if x*2>n then
                exit;
        son:=x*2;
        if (son+1<=n)and(heap[son+1]<=heap[son]) then
                inc(son);
        if (heap[x]>heap[son]) then
        begin
                t:=heap[x];
                heap[x]:=heap[son];
                heap[son]:=t;
        end;
        down(son,n);
end;

procedure insert(x:longint);
var
        fa,t:longint;
begin
        fa:=x div 2;
        if (fa>0)and(heap[fa]>heap[x]) then
        begin
                t:=heap[fa];
                heap[fa]:=heap[x];
                heap[x]:=t;
                insert(fa);
        end;
end;

function delete_root:longint;
begin
        delete_root:=heap[1];
        heap[1]:=heap[n];
        dec(n);
        down(1,n);
end;

begin
        read(n);
        for i:=1 to n do
        begin
                read(heap[i]);
                insert(i);
        end;

        for i:=1 to n-1 do
        begin
                k:=delete_root+delete_root;
                inc(ans,k);
                inc(n);
                heap[n]:=k;
                insert(n);
        end;
        writeln(ans);
end.

7.07 排名:8/19

自动省略水题。

T2 宝石

Description

见上帝动了恻隐之心，天后也想显示一下慈悲之怀，随即从口袋中取出一块魔术方巾，让身边的美神维纳斯拿到后堂的屏风上去试试，屏风是正方形的，高和宽方向上各划有m条鱼屏风的边平行的直线，平行直线间的距离为1厘米。这2m条直线共有m*m个交点，在某些交点上镶嵌着宝石。如果魔术方巾的边与屏风的边平行且魔术方巾触碰到屏风上镶嵌着的宝石，就将与这些宝石等值的金银送给人们。维纳斯想让魔术方巾触碰到的宝石的价值最多，可要在短短的1秒钟之内解决问题，也感到力不从心，你能帮帮她吗？

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Input

输入文件gem.in的第一行有三个正整数m,n,k，数与数之间用一个空格分隔。其中m为屏风在高和宽方向上被划分出的直线数。魔术方巾为正方形的，它的边长为k厘米。N为屏风上宝石的个数。
接下来的n行，每行三个正整数，依次表示宝石所在直线的行号、列号、宝石的价值，数与数之间用一个空格分隔。

Output

输出文件gem.out只有一个正整数，为魔术方巾触碰到的宝石的最大价值总数。

Sample Input

10    4    4
1     1    9
2     3    5
6     2    12
4     5    6

Sample Output

23

只知道是线段树做扫描线,还没有AC。可以参考洛谷主席树第一篇博客的”基础部分:线段树”的那篇博客的最后面的讲解内容。

T3 页

Description

战神阿瑞斯听说2008年在中华大地上，将举行一届规模盛大的奥林匹克运动会，心中顿觉异常兴奋，他想让天马在广阔的天空上，举行一场精彩的天马队列变换表演。首先，战神安排n头高度不同的天马，排成一列。然后重复下面的变换：让中间的天马出列，然后该匹天马可以排在对首，也可以排在队尾，这样称为一次变换，直到出现这一列天马按从低到高的顺序排列为止。那么从初始状态到目标状态最少需要多少次变换呢？你能给战神阿瑞斯参谋参谋吗？

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
Input

输入文件horse.in中有两行，第一行只有一个整数n，表示天马数。
第二行有n个正整数，分别表示n匹天马的高度，每两个数字中间用一个空格分隔。

Output

输出文件horse.out只有一行，该行只有一个正整数，表示从初始状态到目标状态最少需要的变换次数。如果无论如何变换都不能得到从低到高的排列，则输出已行“No Answer”（不包括引号）。

Sample Input

3
179   173  175

Sample Output

2

一开始想到贪心,但是没有证明就做了,最后成功骗取10分。考试过后重新审核,大佬说是搜索。主要是Bfs一遍,然后记录状态看有没有重复搜索,直到第一次达到答案。一些小细节,我们把状态(离散化)压成十进制数,然后存储状态的时候hash一下,最好找一个3000000+的素数来2+次hash。
No answer就是所有状态都弄完了,一般最大有 <= 50000 的状态。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
Uses math;

var
        num,place,Np:array[1..9] of longint;
        sta:array[1..2,1..5677249] of boolean;
        hash:array[1..2] of longint;
        queue,way:array[1..5010000] of longint;
        n,i,head,tail,mid,cup,sort_num,left,right,st1,st2,aa:longint;
        rec:boolean;
        a,b,c,s:string;

procedure Sort(l,r:longint);
var
        i,j,s,t:longint;
begin
        i:=l;
        j:=r;
        s:=num[(l+r) div 2];
        repeat
                while num[i]<s do inc(i);
                while num[j]>s do dec(j);
                if i<=j then
                begin
                        t:=num[i]; num[i]:=num[j]; num[j]:=t;
                        t:=place[i]; place[i]:=place[j]; place[j]:=t;
                        inc(i); dec(j);
                end;
        until i>=j;
        if i<r then Sort(i,r);
        if j>l then Sort(l,j);
end;

procedure ready;
var
        i:longint;
begin
        hash[1]:=4067741;
        hash[2]:=5677249;
        read(n);
        for i:=1 to n do
        begin
                read(num[i]);
                place[i]:=i;
        end;
        Sort(1,n);
        for i:=1 to n do
                inc(sort_num,9*sort_num+i);
        for i:=1 to n do
                num[place[i]]:=i;
        head:=0; tail:=1;
        for i:=1 to n do
                inc(aa,9*aa+num[i]);
        queue[1]:=aa;
        way[1]:=0;
        sta[1,aa mod hash[1]]:=True;
        sta[2,aa mod hash[2]]:=True;
        mid:=n div 2+1;
end;

begin
        ready;
        repeat
                inc(head);
                //writeln(queue[head],' ',way[head]);
                if queue[head]=sort_num then
                begin
                        writeln(way[head]);
                        exit;
                end;

                for i:=n downto 1 do
                begin
                        num[i]:=queue[head] mod 10;
                        queue[head]:=queue[head] div 10;
                end;

                st1:=0;
                st2:=0;
                Np:=num;
                cup:=num[mid];
                for i:=mid downto 2 do
                        num[i]:=num[i-1];
                num[1]:=cup;
                for i:=1 to n do
                        inc(st1,st1*9+num[i]);

                num:=Np;
                cup:=num[mid];
                for i:=mid to n-1 do
                        num[i]:=num[i+1];
                num[n]:=cup;
                for i:=1 to n do
                        inc(st2,st2*9+num[i]);
                if (sta[1,st1 mod hash[1]]=False)and(sta[2,st1 mod hash[2]]=False) then
                begin
                        inc(tail);
                        way[tail]:=way[head]+1;
                        sta[1,st1 mod hash[1]]:=True;
                        sta[2,st1 mod hash[2]]:=True;
                        queue[tail]:=st1;
                end;

                if (sta[1,st2 mod hash[1]]=False)and(sta[2,st2 mod hash[2]]=False) then
                begin
                        inc(tail);
                        way[tail]:=way[head]+1;
                        sta[1,st2 mod hash[1]]:=True;
                        sta[2,st2 mod hash[2]]:=True;
                        queue[tail]:=st2;
                end;
        until head>=tail;
        writeln('No Answer');
end.

T4 景点中心

Description

话说宁波市的中小学生在镇海中学参加计算机程序设计比赛，比赛之余，他们在镇海中学的各个景点参观。镇海中学共有n个景点，每个景点均有若干学生正在参观。这n个景点以自然数1至n编号，每两个景点的编号均不同。每两个景点之间有且只有一条路径。选择哪个景点集中的学生，才能使所有学生走过的路径之和最小呢？

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

输入文件center.in中有若干行：
第一行只有一个正整数n，表示景点数。
第二行有n个1至1000间的整数，这n个整数间互相以一个空格分隔。其中第i个整数表示第i个景点处的学生数。
第三行至第n+1行，每行有三个整数I,j,k，表示景点i和景点j之间有一条长尾k的路径直接连接。其中i<>j,1≤i≤n,1≤j≤n;1≤k≤1000。

Output

输出文件center.out中有二行；
第一行只有一个整数i，表示在第i个景点处集中时，所有学生走过的路径之和最短。
第二行也只有一个整数，表示所有学生走过的路径之和的最小值。

Sample Input

4
3  2  4  1
1  2  5
3  1  6
2  4  4

Sample Output

1
43

因为是一棵树,所以就囧劳枚举,只不过可以用小技巧”换根法”来实现O(1)替换,时间复杂度大大优化。

7.08 排名:17/20

自动省略水题。

T2 电视游戏问题

Description

农夫约翰的奶牛们游戏成瘾！本来FJ是想要按照陶叫兽的做法拿她们去电击戒瘾的，可是后来他发现奶牛们玩游戏之后比原先产更多的奶。很明显，这是因为满足的牛会产更多的奶。 但是，奶牛们在哪个才是最好的游戏平台这个问题上产生了巨大的分歧。一只奶牛想要买一台Xbox 360来跑《光晕3》；另外一只奶牛想要一台任天堂Wii来跑《任天堂明星大乱斗X》；第三只奶牛想要在PlayStation 3上面玩《潜龙谍影4》，顺便还能看某些高画质的日本电影。 FJ想要在给定的预算内购入一些游戏平台和一些游戏，使他的奶牛们生产最多的奶牛以养育最多的孩子。 FJ研究了N（1 <= N <= 50）种游戏平台，每一种游戏平台的价格是P_i（1 <= P_i <= 1000），并且每一种游戏平台有G_i（1 <= G_i <= 10）个只能在这种平台上运行的游戏。很明显，奶牛必须先买进一种游戏平台，才能买进在这种游戏平台上运行的游戏。每一个游戏有一个游戏的价格GP_j（1 <= GP_j 价格 <= 100）并且有一个产出值PV_j（1 <= PV_j<= 1000000），表示一只牛在玩这个游戏之后会产出多少牛奶。 最后，农夫约翰的预算为V（1 <= V <= 100000），即他最多可以花费的金钱。请帮助他确定应该买什么游戏平台和游戏，使得他能够获得的产出值的和最大。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
Input

* 第1行: 两个由空格隔开的整数: N和V
* 第2到第N+1行: 第i+1行表示第i种游戏平台的价格和可以在这种游戏平台上面运行的游戏。包含: P_i, G_i还有G_i对由空格隔开的整数GP_j, PV_j

Output

* 第1行: 农夫约翰在预算内可以得到的最大的产出值。

Sample Input

3 800
300 2 30 50 25 80
600 1 50 130
400 3 40 70 30 40 35 60

Sample Output

210

这道题不就是JM的预算方案吗?可惜我现在还没有A

T3 头晕的奶牛

Description

奶牛们发现，在农场里面赛跑是很有趣的一件事。可是她们一旦在农场里面不断地转圈，就会变得头晕目眩。众所周知，眩晕的奶牛是无法产奶的。于是，农夫约翰想要把他农场里面的双向道路全部改为单向道路，使得他的农场里面一个“圈”都没有，以避免他的奶牛们被搞得晕头转向。如果奶牛可以经过若干条道路回到起点，那么这些道路就称为一个“圈”。 　　农场有N（1 <= N <= 100000）片草地，编号为1到N。这些草地由M1（1 <= M1 <= 100000）条单向道路和M2（1 <= M2 <= 100000）条双向道路连接起来。任何一条道路都不会把一片草地和这篇草地本身连接起来。但是，任意两片草地之间都可能有多条道路连接。不保证任意两片草地之间都有路径相连。 　　你的任务是给所有的双向道路设定一个方向，使得整个农场（只剩下单向道路）最后一个圈都没有。也就是说，不存在一个单向道路序列的终点和起点重合。数据保证一开始就有的单向道路中，一个圈都没有。而且一开始就有的单向道路不能改变。 　　单向道路的起点是草地A_i（1 <= A_i <= N），终点是草地B_i（1 <= B_i <= N）。双向道路连接草地X_i（1 <= X_i <= N）和Y_i（1 <= Y_i <= N）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
Input

　　* 第1行: 三个由空格隔开的正数: N, M1和M2
　　* 第2到1+M1行: 第i+1行表示第i条单向道路，包含两个由空格隔开的整数: A_i和B_i
　　* 第2+M1到第1+M1+M2行: 第i+M1+1行表示第i条单向道路，包含两个由空格隔开的整数X_i和Y_i

Output

　　* 第1到M2行: 第i行应该包含两个由空格隔开的整数: 根据你给第i条双向道路定义的的方向，可能是X_i, Y_i，也可能是Y_i, X_i。这些双向道路必须按照输入的顺序输出。如果无解，在单独的一行内输出"-1"。

Sample Input

4 2 3
1 2
4 3
1 3
4 2
3 2

Sample Output

1 3
2 4
2 3

很强势的拓扑(pu扑)排序,只不过考场没有切。如果l的dep高于r的dep,那么l向r连边,r也去不到l。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
var
        reach,next:array[1..400100] of longint;
        cnt,dep,deg:array[1..200000] of longint;
        i,n,dedge,uedge,l,r,tot:longint;        //directed edge :/: undirected edge\
        head,tail,node:longint;
        queue:array[0..200000] of longint;

procedure add(l,r:longint);
begin
        inc(tot);
        reach[tot]:=r;
        next[tot]:=cnt[l];
        cnt[l]:=tot;
end;

procedure Topological_sort;
var
        i,j:longint;
begin
        node:=0;
        head:=0;
        tail:=0;
        for i:=1 to n do
                if deg[i]=0 then
                begin
                        inc(tail);
                        queue[tail]:=i;
                end;
        repeat
                inc(head);
                inc(node);
                dep[queue[head]]:=node;
                j:=cnt[queue[head]];
                while j<>-1 do
                begin
                        dec(deg[reach[j]]);
                        if deg[reach[j]]=0 then
                        begin
                                inc(tail);
                                queue[tail]:=reach[j];
                        end;
                        j:=next[j];
                end;
        until head>=tail;
end;

begin
        assign(input,'dizzy.in');reset(input);
        assign(output,'dizzy.out');rewrite(output);
        filldword(cnt,sizeof(cnt) div 4,maxlongint*2+1);
        read(n,dedge,uedge);
        for i:=1 to dedge do
        begin
                read(l,r);
                inc(deg[r]);
                add(l,r);
        end;

        Topological_sort;

        for i:=1 to uedge do
        begin
                read(l,r);
                if dep[l]<dep[r] then
                        writeln(l,' ',r)
                else
                        writeln(r,' ',l);
        end;
        close(input);
        close(output);
end.

T4 过路费

Description

跟所有人一样，农夫约翰以着宁教我负天下牛，休叫天下牛负我的伟大精神，日日夜夜苦思生财之道。为了发财，他设置了一系列的规章制度，使得任何一只奶牛在农场中的道路行走，都要向农夫约翰上交过路费。 　　农场中由N（1 <= N <= 250）片草地（标号为1到N），并且有M（1 <= M <= 10000）条双向道路连接草地A_j和B_j（1 <= A_j <= N; 1 <= B_j <= N）。奶牛们从任意一片草地出发可以抵达任意一片的草地。FJ已经在连接A_j和B_j的双向道路上设置一个过路费L_j（1 <= L_j <= 100,000）。 　　可能有多条道路连接相同的两片草地，但是不存在一条道路连接一片草地和这片草地本身。最值得庆幸的是，奶牛从任意一篇草地出发，经过一系列的路径，总是可以抵达其它的任意一片草地。 　　除了贪得无厌，叫兽都不知道该说什么好。FJ竟然在每片草地上面也设置了一个过路费C_i（1 <= C_i <= 100000）。从一片草地到另外一片草地的费用，是经过的所有道路的过路费之和，加上经过的所有的草地（包括起点和终点）的过路费的最大值。 任劳任怨的牛们希望去调查一下她们应该选择那一条路径。她们要你写一个程序，接受K（1<= K <= 10,000）个问题并且输出每个询问对应的最小花费。第i个问题包含两个数字s_i和t_i（1 <= s_i <= N; 1 <= t_i <= N; s_i != t_i），表示起点和终点的草地。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
Input

　　* 第1行: 三个空格隔开的整数: N, M和K
　　* 第2到第N+1行: 第i+1行包含一个单独的整数: C_i
　　* 第N+2到第N+M+1行: 第j+N+1行包含3个由空格隔开的整数: A_j, B_j和L_j
　　* 第N+M+2倒第N+M+K+1行: 第i+N+M+1行表示第i个问题，包含两个由空格隔开的整数s_i和t_i

Output

　　* 第1到第K行: 第i行包含一个单独的整数，表示从s_i到t_i的最小花费。

Sample Input

5 7 2
2
5
3
3
4
1 2 3
1 3 2
2 5 3
5 3 1
5 4 1
2 4 3
3 4 4
1 4
2 3

Sample Output

8
9

我们对每一个点权拍一个序就可以保证正确性了,run floyd,只是要注意我的公式和别的博客的不一样,因为我前面没有加任何处理,T4这里有我写的细节补充。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
Uses math;

var
        dis,ans:array[0..300,0..300] of longint;
        point,NS_point,kk:array[0..300] of longint;
        i,j,n,m,k,l,r,sum,ques:longint;

procedure Clean;
var
        i,j:longint;
begin
        for i:=1 to n do
                for j:=1 to n do
                        if i<>j then
                        begin
                                dis[i,j]:=maxlongint div 843;
                                ans[i,j]:=maxlongint div 843;
                        end;
end;

procedure Sort(l,r:longint);
var
        i,j,s,t:longint;
begin
        i:=l; j:=r; s:=point[(l+r) div 2];
        repeat
                while point[i]<s do i:=i+1;
                while point[j]>s do j:=j-1;
                if i<=j then
                begin
                        t:=point[i]; point[i]:=point[j]; point[j]:=t;
                        t:=kk[i]; kk[i]:=kk[j]; kk[j]:=t;
                        inc(i); dec(j);
                end;
        until i>=j;
        if i<r then Sort(i,r);
        if j>l then Sort(l,j);
end;

begin
        assign(input,'toll.in');reset(input);
        assign(output,'toll.out');rewrite(output);
        read(n,m,ques);
        for i:=1 to n do
        begin
                read(point[i]);
                NS_point[i]:=point[i];
                kk[i]:=i;
        end;
        Sort(1,n);

        Clean;
        for i:=1 to m do
        begin
                read(l,r,sum);
                dis[l,r]:=min(min(dis[l,r],dis[r,l]),sum);
                dis[r,l]:=dis[l,r];
        end;

        for i:=1 to n do
                ans[i,i]:=point[i];
        for k:=1 to n do
                for i:=1 to n do
                        for j:=1 to n do
                        begin
                                dis[i,j]:=min(dis[j,i],min(dis[i,j],dis[i,kk[k]]+dis[kk[k],j]));
                                ans[i,j]:=min(ans[i,j],dis[i,j]+max(point[k],max(NS_point[i],NS_point[j])));
                        end;

        for i:=1 to ques do
        begin
                read(l,r);
                writeln(ans[l,r]);
        end;
        close(input);
        close(output);
end.

7.09 排名:25/29

1
2
3
4
0   【GDOI2003】删边
1       【GDOI2003】骑士问题
2       【GDOI2003】排列的编码
3       【GDOI2003】求值

因为今天的题目都是GDOI,而且十分的水,这里就不详细讲解。

T1

如果可以并查集就用,其实直接输出一个数就可以。m - n + 1

T2

本来看上去像一个过河卒,但是想一想可以Bfs。相当于马的遍历。

T3

康拓展开,字典序也就是全排列,高精度水。

T4

排序之后按i的奇偶来求和。

7.10 排名:12/26

T1 分队问题

Description

给定n个选手，将他们分成若干只队伍。其中第i个选手要求自己所属的队伍的人数大等于a[i]人。 在满足所有选手的要求的前提下，最大化队伍的总数。 注：每个选手属于且仅属于一支队伍。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
Input

第一行一个整数n，表示人数。
以下n行，每行一个整数表示a[i]。

Output

输出队伍总数的最大值。数据保证有解。

Sample Input

5
2
1
2
2
3 

Sample Output

2

Data Constraint

对于20%的数据，n <= 10
对于40%的数据，n <= 1000
对于60%的数据，n <= 10000
对于100%的数据，1 <= n <= 10^6

一开始以为是贪心,然后排序后就拜拜了。结果天不负有心人,40分。然后看向题解,WC?dp?!!

好吧,先正序sort一遍(满足大的需求),然后dp,ans[i]:=max{ans[1],ans[2]..ans[i-num[i]]}+1。就算对于我这个dp馄饨也是可以想到的。然后再想一想,max??O(n^2)。不炸就真的见怪了。然后弄一个前缀和,这题就结束了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
Uses math;

var
        i,j,n:longint;
        ans,num,maxn:array[0..1000010] of longint;

procedure Sort(l,r:longint);
var
        i,j,s,t:longint;
begin
        i:=l; j:=r; s:=num[(l+r) div 2];
        repeat
                while num[i]<s do i:=i+1;
                while num[j]>s do j:=j-1;
                if i<=j then
                begin
                        t:=num[i]; num[i]:=num[j]; num[j]:=t;
                        inc(i); dec(j);
                end;
        until i>=j;
        if i<r then Sort(i,r);
        if j>l then Sort(l,j);
end;

begin
        read(n);
        for i:=1 to n do
                read(num[i]);
        Sort(1,n);
        for i:=1 to n do
        begin
                ans[i]:=maxn[i-num[i]]+1;
                maxn[i]:=max(maxn[i-1],ans[i]);
        end;
        writeln(ans[n]);
end.

T2 数字对

Description

对于一个数字对(a, b)，我们可以通过一次操作将其变为新数字对(a+b, b)或(a, a+b)。 给定一正整数n，问最少需要多少次操作可将数字对(1, 1)变为一个数字对，该数字对至少有一个数字为n。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
Input

第一行一个正整数 n

Output

    一个整数表示答案。

Sample Input

5

Sample Output

3

Data Constraint

    对于30%的数据， 1 <= n <= 1000
    对于60%的数据， 1 <= n <= 20000
    对于100%的数据，1 <= n <= 10^6 100万

Hint

【样例解释】
(1,1)  →  (1,2)  →  (3,2)  →  (5,2)

哇,这不是水题吗,这不是和前几天的’页’差不多嘛?Bfs一遍无人可当。不过看一下数据,就不论玄不玄了。

这道题可以反过来推算。假如b>a,(a,b)->(a,b+a) or (a+b,b)就可以转换为:(a,b)<-(a,b-a)。然后n的话就全部推算一遍就OK了。(a+b=n,循环一遍,求最小值)

就算到达了这种思想境界,我们还是会超时。所以想到了类似于GCD的做法,看一下这个例子:

1
2
3
4
5
(1,99)
(1,98) (99-1)
(1,97) (98-1)
.......
(1,1) 结束

这不是贼慢了,我们就直接b mod a就可以了呀(注意a>b),那么它们相除的次数就是b div a。此题非数论,完全找规律。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
Uses math;

var
        n,i,a,b,ans,o:longint;
begin
        o:=maxlongint;
        read(n);
        for i:=1 to n-1 do
        begin
                a:=i;
                b:=n-i;
                ans:=0;
                repeat
                        if a>b then
                        begin
                                inc(ans,a div b);
                                a:=a mod b;
                        end
                        else
                        begin
                                inc(ans,b div a);
                                b:=b mod a;
                        end;
                        if (a=0)or(b=0) then
                                break;
                until (a<=1)and(b<=1);
                if (a=1)or(b=1) then
                        o:=min(ans,o);
        end;
        writeln(o);
end.
``` 
## T3 高级打字机
### Description
``
早苗入手了最新的高级打字机。最新款自然有着与以往不同的功能，那就是它具备撤销功能，厉害吧。
请为这种高级打字机设计一个程序，支持如下3种操作：
T x：在文章末尾打下一个小写字母x。(type操作)
U x：撤销最后的x次修改操作。（Undo操作）（注意Query操作并不算修改操作）
Q x：询问当前文章中第x个字母并输出。（Query操作）文章一开始可以视为空串。
``

Input

第1行：一个整数n，表示操作数量。
以下n行，每行一个命令。保证输入的命令合法。

Output

每行输出一个字母，表示Query操作的答案。

Sample Input

7
T a
T b
T c
Q 2
U 2
T c
Q 2

Sample Output

b
c

Data Constraint

对于40%的数据 n<=200;
对于100%的数据 n<=100000；保证Undo操作不会撤销Undo操作。
<高级挑战>
对于200%的数据 n<=100000；Undo操作可以撤销Undo操作。

<IOI挑战>
必须使用在线算法完成该题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87

看到IOI挑战就GG了,此题必~~切~~。然后打了一个100%的程序,~~只得了50分~~。

此题200%是持久化数组,用于各种历史版本。幸好的是之前就学了主席树,现在改起来非常方便,详情请见我的主席树博客。

补充:此题是可持久化数组,运用主席树的时候,只用对叶子节点进行赋值。

```pascal
var
        n,cnt,hao,tot:longint;
        len,lson,rson,root:array[0..2000035] of longint;
        value:array[0..2000035] of char;
        s:string;
        HuHa:char;

procedure build(var rt:longint; fa,l,r,po:longint);
var
        mid:longint;
begin
        if (rt=0) then
        begin
                inc(tot);
                rt:=tot;
        end;
        if l=r then
        begin
                value[rt]:=HuHa;
                exit;
        end;

        mid:=(l+r) div 2;
        if (po<=mid) then
        begin
                rson[rt]:=rson[fa];
                build(lson[rt],lson[fa],l,mid,po);
        end;
        if (po>=mid+1) then
        begin
                lson[rt]:=lson[fa];
                build(rson[rt],rson[fa],mid+1,r,po);
        end;
end;

function Query(rt,l,r,po:longint):char;
var
        mid:longint;
begin
        if l=r then
                exit(value[rt]);
        mid:=(l+r) div 2;
        if (po<=mid) then
                exit(Query(lson[rt],l,mid,po));
        if (po>=mid+1) then
                exit(Query(rson[rt],mid+1,r,po));
end;

begin
        readln(n);
        while n>0 do
        begin
                readln(s);
                if s[1]='T' then
                begin
                        HuHa:=s[3];
                        inc(cnt);
                        len[cnt]:=len[cnt-1]+1;
                        Build(root[cnt],root[cnt-1],1,100007,len[cnt]);
                end;

                if s[1]='U' then
                begin
                        delete(s,1,2);
                        val(s,hao);
                        inc(cnt);
                        len[cnt]:=len[cnt-hao-1];
                        root[cnt]:=root[cnt-hao-1];
                end;

                if s[1]='Q' then
                begin
                        delete(s,1,2);
                        val(s,hao);
                        writeln(Query(root[cnt],1,100007,hao));
                end;
                dec(n);
        end;
end.

7.11 排名:10/20

T1 气象牛

Description

为了研究农场的气候,Betsy帮助农夫John做了N(1 <= N <= 100)次气压测量并按顺序记录了结果M_1...M_N(1 <= M_i <= 1,000,000). 　　Betsy想找出一部分测量结果来总结整天的气压分布. 她想用K(1 <= K <= N)个数s_j (1 <= s_1 < s_2 < ... < s_K <= N)来概括所有测量结果. 她想限制如下的误差: 　　对于任何测量结果子集,每一个非此子集中的结果都会产生误差.总误差是所有测量结果的误差之和.更明确第说, 对于每一个和所有s_j都不同的i: 　　* 如果 i 小于 s_1, 误差是:2 * | M_i - M_(s_1) | 　　* 如果i在s_j和s_(j+1)之间,误差是:| 2 * M_i - Sum(s_j, s_(j+1)) | 　　注:Sum(x, y) = M_x + M_y; (M_x 和 M_y 之和) 　　* 如果i大于s_K,误差为:2 * | M_i - M_(s_K) | 　　Besty给了最大允许的误差E (1 <= E <= 1,000,000),找出最小的一部分结果使得误 差最多为E. 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Input
　　第一行: 两个空格分离的数: N 和 E
　　第2..N+1行: 第i+1行包含一次测量记录:M_i

Output
　　第一行: 两个空格分开的数: 最少能达到误差小于等于E的测量数目和使用那个测量数目能达到的最小误差.

Sample Input
4 20
10
3
20
40

Sample Output
2 17

Hint
【样例说明】
　　选择第二和第四次测量结果能达到最小误差17. 第一次结果的误差是2*|10-3| = 14;第三次结果的误差是|2*20 - (3+40)|=3.

一眼dp,我是不会A的。

T2 轻轨

Description

有N（1<=N<=20,000）个站点的轻轨站，有一个容量为C（1<=C<=100）的列车起点在1号站点，终点在N号站点，有K(K<=50,000)组牛群，每组数量为M_i（1<=M_i<=N），行程起点和终点分别为S_i和E_i（1<=S_i<E_i<=N） 　　计算最多有多少头牛可以搭乘轻轨。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
Input
　　第1行：3个空格隔开的整数K,N,C
　　第2到K+1行：描述每组奶牛的情况，每行3个空格隔开的整数S_i,E_i和M_i

Output
　　输出一个整数表示最多可以搭乘轻轨的牛的数量。

Sample Input
8 15 3
1 5 2
13 14 1
5 8 3
8 14 2
14 15 1
9 12 1
12 15 2
4 6 1

Sample Output
10

Hint
【样例说明】
　　轻轨从1号站搭2头牛到5号站，搭3头牛从5好站到8号站，2头牛从8号站到14号站，1头牛从9号站到12号站，1头牛从13号站到14号站，1头牛从14号站到15号站。

贪心+线段树优化,现在正在码。

T3 设计

Description

和人一样，牛也喜欢站得离朋友较近的位置。FJ有N(2<=N<=1,000)头牛，编号为1..N,现在要设计一个顺序让他们站成一排给他们喂食。奶牛们按照编号顺序依次站立，允许有多只牛站在同一位置（也就是说，牛i和牛j(i<j)的站立位置s_i,s_j一定满足s_i<=s_j,如果s_i=s_j,那么编号为i到j之间的牛也一定站在s_i处）。 　　有一些牛相互喜欢，希望两人的距离在某个范围内，同样也有一些牛相互不喜欢，希望两人的距离大于等于某个距离，题目中给出ML(1<=ML<=10,000)个限制描述相互喜欢的情况，给出MD(1<=MD<=10,000)个限制描述相互不喜欢的情况。 　　你的任务是计算，如果存在某种方案满足上述要求，输出1号牛和N号牛之间最大距离。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
Input
　　第1行：3个空格隔开的整数N,ML,MD。
　　第2到ML+1行：每行包含3个空格隔开的整数A,B和D，满足1<=A<B<=N,表示牛A和牛B之间的距离不得超过D(1<=D<=1,000,000)。
　　第ML+2到ML+MD+1行：每行包含3个空格隔开的整数A,B和D，满足1<=A<B<=N,表示牛A和牛B之间的距离至少为D(1<=D<=1,000,000)。

Output
　　如果不存在这样的方案，输出-1，如果牛1和牛N之间的距离可以任意，输出-2，否则输出最大的距离。

Sample Input
4 2 1
1 3 10
2 4 20
2 3 3

Sample Output
27

Hint
【样例说明】

好,来细细讲一下图论差分约束。参考:blog

首先,我们看题中每一个牛互相有一个想要靠近值和不想靠近值。我一开始就用数轴进行画图,然后证明靠近与不靠近的影响,感觉没有影响。
然后按照数轴打Floyd,不同于的是,我是这样子打的:(i<k<j)

1
2
3
4
5
6
if (table[i,k]>0)and(table[k,j]>0) then
        table[i,j]:=max(table[i,j],table[i,k]+table[k,j]);
if (table[i,j]>0)and(table[k,j]>0) then
        table[i,k]:=max(table[i,k],table[i,j]-table[k,j]);
if (table[i,j]>0)and(table[i,k]>0) then
        table[k,j]:=max(table[k,j],table[i,j]-table[i,k]);

符合一个数轴的解法,有点像前几天的“矩阵”。

天不负有心人,还是拿了10分。好吧,正式开始差分约束。

我们有条件,j>=i,而且 dis[j]-dis[i]>=len(这是不喜欢的情况,>=距离,喜欢就是dis[j]-dis[i]<=len)这是肯定的。

我们运用一下不等式的知识: dis[j]>=len+dis[i] dis[j]<=len+dis[i],这就转化为一个松弛操作。

附上大佬云:“上面的代码要实现的是使dis[i]+len>dis[k],而对于不等式，我们进行建边的操作：对于每个不等式 dis[i] - dis[j] <= len，对结点 j 和 i 建立一条 j -> i的有向边，边权为len，求dis[n] - dis[1] 的最大值就是求 1 到n的最短路，两者刚好吻合。所以求解差分约束问题就转化为了最短路问题。”

好了,现在讲完了差分约束的一致思路,讲一讲实现:

1
2
3
4
1.如果两只牛互相喜欢,那么l->r建立一条边权为sum的边。注意r>=l,输入的时候判断一下,swap。
2.如果两只牛互相讨厌,那么r->l建立一条边权为-sum的边(思路如上)。注意r>=l
3.编号临近(i和i-1)的牛 i->i-1 (或者i+1->i) 建立一条边权为0的边。
4.跑最短路,注意要用spfa或者其它来判负环。如果long(答案)[n]=maxlongint的话,输出-2。

附上Code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
Uses math;
var
        n,m,i,start,l,r,sum,head,tail,now,k:longint;
        long,cnt,way:array[0..10100] of longint;
        will:array[0..500100] of longint;
        ask:array[0..10000] of boolean;
        next,right,val:array[0..50010] of longint;

procedure swap(var a,b:longint);
var
        t:longint;
begin
        if b<a then
        begin
                t:=a;
                a:=b;
                b:=t;
        end;
end;

procedure add(x,y,sum:longint);
begin
        inc(now);
        right[now]:=y;
        val[now]:=sum;
        next[now]:=cnt[x];
        cnt[x]:=now;
end;

procedure read_;
var
        i,md,ml:longint;
begin
        start:=1;
        read(n,md,ml);
        for i:=1 to md do
        begin
                read(l,r,sum);
                if r>l then
                        swap(l,r);
                add(l,r,sum);
        end;
        for i:=1 to ml do
        begin
                read(l,r,sum);
                if r>l then
                        swap(l,r);
                add(r,l,-sum);
        end;
        for i:=2 to n do
                add(i,i-1,0);

        ask[start]:=True;
        head:=1;
        tail:=1;
        will[1]:=start;
        way[1]:=0;
        long[start]:=0;
end;

procedure SPFA;
begin
        repeat
                l:=will[head];
                inc(head);
                ask[l]:=False;
                k:=cnt[l];
                while k<>-1 do
                begin
                        if (long[l]+val[k]<=long[right[k]]) then
                        begin
                                way[right[k]]:=way[l]+1;
                                if way[right[k]]>n then
                                begin
                                        writeln(-1);
                                        halt;
                                end;
                                long[right[k]]:=long[l]+val[k];
                                if ask[right[k]]=False then
                                begin
                                        inc(tail);
                                        ask[right[k]]:=True;
                                        will[tail]:=right[k];
                                end;
                        end;
                        k:=next[k];
                end;
        until head>tail;
        if long[n]>maxlongint div 843 then
                writeln(-2)
        else
                writeln(long[n]);
end;

begin
        fillchar(long,sizeof(long),127);
        fillword(cnt,sizeof(cnt),maxlongint*2+1);
        fillchar(ask,sizeof(ask),False);
        Read_;
        SPFA;
end.

7.12 排名:完美垫底

T1 序章-弗兰德的秘密

Description

弗兰德最高的两棵树，只要知道两棵树的共同的相似度就行了…… 给定两棵有根树，可以任意删除两棵树上的节点（删除一棵节点必须保证该节点的子树内的所有节点也必须要被删除，换一种说法，删除后的树必须联通并形成一棵树，且根节点不能被删除），使得删除后的两棵树同构，这两棵树有一个共同大小，即树的size，最大化同构的树的size即为机关的答案……注：两棵同构的树要满足以下条件： 1、两棵树节点个数相等。 2、两棵树的以根节点的儿子为根子树对应同构。如下图，为两棵同构的有根树。 如下图，为两棵同构的有根树。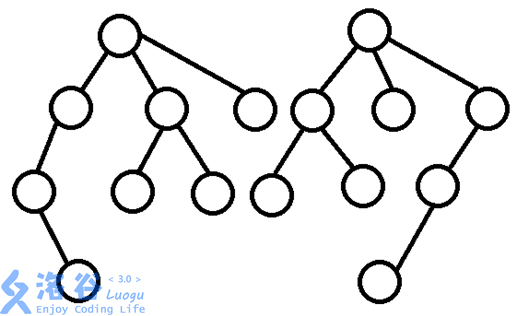

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
Input
一行两个整数n,m分别表示两棵有根树的大小。
以下n-1行描述第一棵树，每行两个数x,y表示x号节点是y号节点父亲。
以下m-1行描述第二棵树，每行两个数x,y表示x号节点是y号节点父亲。
数据保证两棵树的1号节点均为根。

Output
一行一个数，表示两棵树的相似度（删除后最大化的同构树的大小）。

Sample Input
3 3
1 2
1 3
1 2
2 3

Sample Output
2
【样例解释】
第一棵树可以保留1号节点和2号节点删除3号节点，也可以保留1号节点与3号节点删除2号节点，
第二棵树保留1号节点和2号节点删除3号节点。
剩下的树同构，树的节点个数均为2。

Data Constraint
对于30%的数据，1 ≤ n ≤10
对于60%的数据，1 ≤ n ≤ 100
对于100%的数据，1 ≤ n ≤ 1000数据保证两棵树上每个节点的度均不超过5。

一开始以为可以用son的顺序来水字典树之类的东西来做标记,来判断。正解是树形Dp。

T2 圣章-精灵使的魔法语

Description

上述剧情省略。 我没兴趣地瞟了一眼，“哼。这种东西我不看也会，伦福萨——密西卡！”... 喂喂喂，别往我这边看啊，我有视线恐惧症啊！！！！况且，我只是把她正在吃的面包的样子变成虫子而已，谁会料到这种情况啊啊啊！！ “里修！你……”她从牙缝里挤出了一个字。我顿感不妙，见到了那张比魔鬼还可怕的扭曲的面孔。“真是个魔法的天才哪！”她一扫之前不愉快的表情，想我露出大拇指，好像是在夸奖我的样子。

“伦福萨”【即" ( "】和“密西卡”【即" ) "】是两种不同的精灵咒语，已知一个成功的咒语符合如下的规定： 每一个密西卡之前都可以对应匹配到一个伦福萨，即为一个合法的精灵魔法咒语。 方便的是，我们将“伦福萨”视为" ( "，“密西卡”视为" ) "，合法的精灵魔法咒语即为一个合法的括号序列。 如：" ( ( ( ) ) ) "" ( ( ) ( ) ) "" ( ) ( ) ( ) "均为合法的魔法咒语，" ) ( "" ( ) ) ( "" ( ( "均为不合法的魔法咒语。 现在弗洛莉给我一个长长的“伦福萨”【即" ( "】和“密西卡”【即" ) "】的片段，每次给我一个l和r，让我判断需要在这个片段前最少添多少个“伦福萨”【即" ( "】，以及最少添多少个“密西卡”【即" ) "】可以成为一个合法的魔法咒语，更令人不爽的是，弗洛莉有的时候还会把一个“伦福萨”【即" ( "】变成“密西卡”【即" ) "】，或把一个“密西卡”【即" ) "】变为“伦福萨”【即" ( "】。

一眼看到”(()()(“,就想到了栈的解法和递归的解法。然后想到区间,就是用线段树。但是考场上的线段树就是乱打的,维护的就是区间括号类型数量。

后来看了题解,线段树维护的值就是答案:区间内需要增加的左括号数量和需要增加的右括号数量。其中需要增加的右括号数量也可以转化为多余的左括号数量,思考一下即可得出。(need为需要增加的左括号数量,而surplus为多余的左括号数量)

首先解决叶子节点的问题。叶子节点存什么?如果s(ansistring)[i]=’(‘的话就存上need[k]:=1,’)’则存上surplus[k]:=1。

其次我们在区间上维护子节点的时候,有一个公式,可以慢慢思考:

1
2
need[k]:=need[k*2]+max(need[k*2+1]-surplus[k*2],0);
surplus[k]:=surplus[k*2+1]+max(surplus[k*2]-need[k*2+1],0);

这个公式运用在Make_tree建树上和Change修改上。博客上有解释,这里不细讲。

本道题目很多细节,所以我觉得打注释。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
//Title:T2 圣章-精灵使的魔法语

Uses math;

var
        need,surplus:array[0..610000] of longint; //上述讲解
        ans,ask:array[1..2] of longint; //答案与询问(Query的第1,2个数和Change的第1个数)
        n,m,i,x,y,k,l,r:longint; //某些变量
        s,kk:ansistring;
        a:char;

procedure make(l,r,k:longint); //Make_tree
var
        mid:longint;
begin
        if l=r then 
        begin
                if kk[l]='(' then surplus[k]:=1 //上述
                else  need[k]:=1;
                exit;
        end;
        mid:=(l+r) div 2;
        make(l,mid,k*2);
        make(mid+1,r,k*2+1);
        need[k]:=need[k*2]+max(need[k*2+1]-surplus[k*2],0); //子树的值改变,运用公式
        surplus[k]:=surplus[k*2+1]+max(surplus[k*2]-need[k*2+1],0);
end;

procedure query(l,r,k,x,y:longint); //注意我们存储了x,y这对目标变量
var
        mid:longint;
begin
        if (x=l)and(r=y) then
        begin
                inc(ans[1],max(need[k]-ans[2],0)); //注意,一个是inc(c++:"+="),一个是赋值
                ans[2]:=surplus[k]+max(ans[2]-need[k],0);
                exit;
        end;
        if l=r then //某种加快操作
                exit;

        mid:=(l+r) div 2;
        if y<=mid then //3种情况,其中最后一种的2个转移,目标也转移
                query(l,mid,k*2,x,y)
        else
        if x>mid then
                query(mid+1,r,k*2+1,x,y)
        else
        begin
                query(l,mid,k*2,x,mid);
                query(mid+1,r,k*2+1,mid+1,y);
        end;
end;

procedure change(l,r,k:longint);
var
        mid:longint;
begin
        if (l=r) then
        begin
                if need[k]=1 then //改变括号类型
                begin
                        need[k]:=0;
                        surplus[k]:=1;
                end
                else
                begin
                        need[k]:=1;
                        surplus[k]:=0;
                end;
                exit;
        end;

        mid:=(l+r) div 2;
        if x<=mid then //只有两种,注意目标只有一个
                change(l,mid,k*2)
        else
                change(mid+1,r,k*2+1);

        need[k]:=need[k*2]+max(need[k*2+1]-surplus[k*2],0); //子树的值发生改变,公式
        surplus[k]:=surplus[k*2+1]+max(surplus[k*2]-need[k*2+1],0);
end;

function work(s:ansistring):longint;//取出2(1)个数/上述,C++选手自动跳过
var
        bz:boolean;
        i,j,k:longint;
begin
        ask[1]:=0;
        ask[2]:=0;
        k:=0;
        bz:=True;
        for i:=1 to length(s) do
                if (s[i]>='0')and(s[i]<='9') then
                begin
                        val(s[i],j);
                        inc(ask[k],ask[k]*9+j);
                        bz:=True;
                end
                else
                if bz then
                begin
                        bz:=False;
                        inc(k);
                end;
        if ask[2]>0 then
                exit(1);
        exit(0);
end;

begin
        assign(input,'elf.in');reset(input); //某种文操
        assign(output,'elf.out');rewrite(output);
        readln(n,m);
        readln(kk);
        make(1,n,1);
        for i:=1 to m do
        begin
                readln(s);
                if work(s)=1 then
                begin
                        ans[1]:=0;//答案
                        ans[2]:=0;
                                                x:=ask[1];
                        y:=ask[2];
                                                query(1,n,1,x,y);
                        writeln(ans[1],' ',ans[2]);
                end
                else
                begin
                        x:=ask[1];
                        change(1,n,1);
                end;
        end;
        close(input);
        close(output);
end.
//因为pascal的蓝色背景,所以一直用sublime打pascal,所以缩进有一点问题,并不是我打的chou

T3 终章-剑之魂

My soul of my sowrd! 终焉的试炼即将到来，作为一名有修养的剑士，虽然没有习得n刀流但是二刀流还是没问题的。然而我也是个剑的收藏者，家里屯着n把剑，每一把剑都有一个灵魂值a[i]，由于一些剑之间可能有共鸣，所以我需要两把契合度最高的剑。据剑圣所说，两把编号为i,j剑的契合度为a[i] and a[j]。如何深得剑的灵魂呢？(注：AND 为按位与运算，先将数转成二进制，不满位数的补全0，然后成为两个长度相同的二进制数，处理的时候，两个相应的二进制位都为1，该位的结果值才为1，否则为0。)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
Input
第一行一个整数n，代表藏剑数。
第二行n个整数，第i个整数表示a[i]。

Output
输出包含一个正整数，最好的两把剑的契合度。

Sample Input
5
12 5 6 3 1

Sample Output
4
【样例解释】
5 and 6=4或者12 and 5=4或者12 and 6=4

Data Constraint
对于40%的数据 n ≤ 1,000
对于100%的数据 n ≤ 1,000,000，0 ≤ a[i] < 2^31

看一下数据就可以得到暴力可以40分(而不是想数论)。我看着看着找到一个非常神奇的规律:如果a[i]和a[j]都是最大,或者是次..次次..次次次大的…并且保证a[i]和a[j]是同一个log层里面的,那么这个就是有可选性的答案。天不负有心人,20分成功被对手绝杀。

这一题可以用某个大佬的数论过,我讲一下另一种简单的数论:先看一个定理:

1
a and b <= max(a,b)

我们做出猜想,假设a和b是最大的,那么a and b才会大。

然后就出现了这种做法:

1
2
3
4
5
6
7
8
1.Sort(a[1],a[2]...a[i]...a[n]); (从小到大或者从大到小要根据下面的步骤)
2.(如果是从小到大,从大到小相反)
for i:=n downto 1 do
        for j:=i-1 downto 1 do
        if ans<a[i] and a[j] then
                ans:=a[i] and a[j]
        else
      -->break;

排序就是为了这个break,仔细想一想,还是线性复杂度。

1
2
理论复杂度:O(n log n+n^2) --> O(n^2)
实际复杂度:O(n log n+n(乘1)) --> O(n log n)

B-Group T1 挑竹签 (乱入)

Description

挑竹签——小时候的游戏 夏夜，早苗和诹访子在月光下玩起了挑竹签这一经典的游戏。 挑竹签，就是在桌上摆上一把竹签，每次从最上层挑走一根竹签。如果动了其他的竹签，就要换对手来挑。在所有的竹签都被挑走之后，谁挑走的竹签总数多，谁就胜了。 身为神明的诹访子自然会让早苗先手。为了获胜，早苗现在的问题是，在诹访子出手之前最多能挑走多少竹签呢？ 为了简化问题，我们假设当且仅当挑最上层的竹签不会动到其他竹签。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
Input
输入文件mikado.in。
第一行输入两个整数n,m, 表示竹签的根数和竹签之间相压关系数。
第二行到m+1 行每行两个整数u,v，表示第u 根竹签压住了第v 根竹签。

Output
输出文件mikado.out。
一共一行，一个整数sum，表示最多能拿走sum 根竹签。

Sample Input
6 6
1 2
2 3
3 1
4 3
4 5
6 5

Sample Output
3
样例解释：
一共有6 根竹签，其中1 压住2，2 压住3，3 压住1，4 压住3 和5，6 压住5。最优方案中，我们可以依次挑走4、6、5 三根竹签。而剩下的三根相互压住，都无法挑走。所以最多能挑走3 根竹签。

Data Constraint
对于20% 的数据，有1<= n,m<= 20。
对于40% 的数据，有1 <= n,m <= 1 000。
对于100% 的数据，有1 <= n,m <= 1 000 000。

这道题可以转换为判环问题。然后我们想到一种不用那么多Dfs有可行的方案——可以拓补排序! 如果节点有dep则这个点可以挑。一开始看题目看成B组,瞬间想到T1正解。

感想

以后不打贪心就可以了,要花一些时间来证正确性——It is important all for us.

7.13 排名:垫底

T1 七夕祭

Description

七夕节因牛郎织女的传说而被扣上了「情人节」的帽子。于是TYVJ今年举办了一次线下七夕祭。Vani同学今年成功邀请到了cl同学陪他来共度七夕，于是他们决定去TYVJ七夕祭游玩。TYVJ七夕祭和11区的夏祭的形式很像。矩形的祭典会场由N排M列共计N×M个摊点组成。虽然摊点种类繁多，不过cl只对其中的一部分摊点感兴趣，比如章鱼烧、苹果糖、棉花糖、射的屋……什么的。Vani预先联系了七夕祭的负责人zhq，希望能够通过恰当地布置会场，使得各行中cl感兴趣的摊点数一样多，并且各列中cl感兴趣的摊点数也一样多。 不过zhq告诉Vani，摊点已经随意布置完毕了，如果想满足cl的要求，唯一的调整方式就是交换两个相邻的摊点。两个摊点相邻，当且仅当他们处在同一行或者同一列的相邻位置上。由于zhq率领的TYVJ开发小组成功地扭曲了空间，每一行或每一列的第一个位置和最后一个位置也算作相邻。现在Vani想知道他的两个要求最多能满足多少个。在此前提下，至少需要交换多少次摊点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
Input
第一行包含三个整数N和M和T。T表示cl对多少个摊点感兴趣。

接下来T行，每行两个整数x, y，表示cl对处在第x行第y列的摊点感兴趣。

Output
首先输出一个字符串。如果能满足Vani的全部两个要求，输出both；如果通过调整只能使得各行中cl感兴趣的摊点数一样多，输出row；如果只能使各列中cl感兴趣的摊点数一样多，输出column；如果均不能满足，输出impossible。

如果输出的字符串不是impossible， 接下来输出最小交换次数，与字符串之间用一个空格隔开。

Sample Input
样例输入1

2 3 4

1 3

2 1

2 2

2 3

样例输入2

3 3 3

1 3

2 2

2 3

Sample Output
样例输出1

row 1

样例输出2

both 2

Data Constraint
对于30% 的数据，N, M≤100。

对于70% 的数据，N, M≤1000。

对于100% 的数据，1≤N, M≤100000，0≤T≤min(NM, 100000)，1≤x≤N，1≤y≤M。

大佬题解:稍加思索可以发现，行列之间是互不影响的，把每行 1 的个数看做 n 堆纸牌、每列 1 的个数
看做 m 堆纸牌，题目实际上就是两个环形的均分纸牌问题。
(什么？你不知道均分纸牌问题！你还是看看 NOIP2002 T1，做做历届 NOIP 前两题再来
吧……)

下面来说环形均分纸牌问题怎么做：
设有 n 堆纸牌，每堆有 ai 张，所有堆一共有 s 张，那么最终每堆应该有 s / n 张。因此如果 s
mod ai≠0，显然是无解的。接下来构造数列 bi=ai-s/n。

方法一：
枚举从第 k 个位置开始(1<=k<=n)，像均分纸牌的方法一样依次向后推（如果第 i 个位置有
ai 堆牌，那么取 bi 堆牌分给下一堆，若 bi<0 表示从下一堆拿到这一堆）。最后取最小值。
时间复杂度 O(n^2)，预计得分 70 分。
方法二：

设 bi 的前缀和为 si。如果从第 k 个位置开始，那么第 i 堆和第 i+1 堆交换的纸牌数就是 |si-sk|。
总代价就是|s1-sk|+|s2-sk|+|s3-sk|+……+|sn-sk|。发现什么了？当 sk 是 s1~sn 中位数的时候，
上式有最小值！所以把 si 排序后，令 sk=s[(n+1)/2]，计算代价即可。
时间复杂度 O(nlogn)，预计得分 100 分。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
var
        a,b,h,l,c:array[-1..1000100] of longint;
        i,j,n,m,k,t,mid:longint;
        ans:int64;

procedure Sort(l,r:longint);
var
        i,j,s,t:longint;
begin
        i:=l; j:=r; s:=c[(l+r) div 2];
        repeat
                while c[i]<s do i:=i+1;
                while c[j]>s do j:=j-1;
                if i<=j then
                begin
                        t:=c[i]; c[i]:=c[j]; c[j]:=t;
                        inc(i); dec(j);
                end;
        until i>=j;
        if i<r then Sort(i,r);
        if j>l then Sort(l,j);
end;

begin
        ans:=0;
        read(n,m,t);
        k:=t div n;
        for i:=1 to t do
        begin
                read(a[i],b[i]);
                inc(h[a[i]]);
                inc(l[b[i]]);
        end;

        if t mod n=0 then
        begin
                for i:=1 to t do
                        c[i]:=c[i-1]+h[i]-t div n;
                Sort(1,n);
                mid:=c[(n+1) div 2];
                for i:=1 to n do
                        inc(ans,abs(c[i]-mid));
        end;
        if t mod m=0 then
        begin
                fillchar(c,sizeof(c),0);
                for i:=1 to t do
                        c[i]:=c[i-1]+l[i]-t div m;
                Sort(1,m);
                mid:=c[(m+1) div 2];
                for i:=1 to m do
                        inc(ans,abs(c[i]-mid));
        end;

        if (t mod n<>0)and(t mod m<>0) then
                writeln('impossible')
        else
        if (t mod n<>0)and(t mod m=0) then
                writeln('column ',ans)
        else
        if (t mod n=0)and(t mod m<>0) then
                writeln('row ',ans)
        else
                writeln('both ',ans);
end.

T2 太鼓达人

Description

七夕祭上，Vani牵着cl的手，在明亮的灯光和欢乐的气氛中愉快地穿行。这时，在前面忽然出现了一台太鼓达人机台，而在机台前坐着的是刚刚被精英队伍成员XLk、Poet_shy和lydrainbowcat拯救出来的的applepi。看到两人对太鼓达人产生了兴趣，applepi果断闪人，于是cl拿起鼓棒准备挑战。然而即使是在普通难度下，cl的路人本性也充分地暴露了出来。一曲终了，不但没有过关，就连鼓都不灵了。Vani十分过意不去，决定帮助工作人员修鼓。 鼓的主要元件是M个围成一圈的传感器。每个传感器都有开和关两种工作状态，分别用1和0表示。显然，从不同的位置出发沿顺时针方向连续检查K个传感器可以得到M个长度为K的01串。Vani知道这M个01串应该是互不相同的。而且鼓的设计很精密，M会取到可能的最大值。现在Vani已经了解到了K的值，他希望你求出M的值，并给出字典序最小的传感器排布方案。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Input
一个整数K。

Output
一个整数M和一个二进制串，由一个空格分隔。表示可能的最大的M，以及字典序最小的排布方案，字符0表示关，1表示开。
你输出的串的第一个字和最后一个字是相邻的。

Sample Input
3

Sample Output
8 00010111

样例解释：

得到的8个01串分别是000、001、010、101、011、111、110和100。注意前后是相邻的。
长度为3的二进制串总共只有8种，所以M = 8一定是可能的最大值。

Data Constraint
对于全部测试点，2≤K≤11。

这道题就是爆搜,也可以用欧拉回路跑一遍。讲一讲爆搜的主要思路。

如果两个字典序的全排列(类似)的后两位和前两位是一样的,我们就选入。表示为:if num[i,后两位]=num[i+1…n,前两位] then:选入。

细节见Code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
//Title:太鼓达人

var
        n,i,j,tail,len,k,o:longint;
        num:array[0..110000] of string;
        used:array[0..110000] of boolean;
        ans:string;

procedure Dfs(x:longint;s:string);
var
        i:longint;
begin
        if x=n+1 then
        begin
                inc(tail);
                num[tail]:=s;
                exit;
        end
        else
        begin
                Dfs(x+1,s+'0');
                Dfs(x+1,s+'1');
        end;
end;

procedure Dfs2(x:longint;ans:ansistring);
var
        j:longint;
begin
        if x=len then
        begin
                for i:=1 to length(ans)-n+1 do
                        write(ans[i]);
                halt;
        end;
        for j:=2 to len do
                begin
                        if used[j]=False then
                        begin
                                o:=0;
                                used[0]:=True;
                                for k:=length(ans)-n+2 to length(ans) do
                                begin
                                        inc(o);
                                        if ans[k]<>num[j,o] then
                                        begin
                                                used[0]:=False;
                                                break;
                                        end;
                                end;
                                if used[0] then
                                begin
                                        used[j]:=True;
                                        Dfs2(x+1,ans+num[j,n]);
                                        used[j]:=False;
                                end;
                        end;
                end;
end;

begin
        read(n);
        len:=1 << n;
        write(len,' ');
        Dfs(1,'');

        for i:=1 to n do
                ans:=ans+'0';
        Dfs2(1,ans);
end.

T3 理科男

Description

“那么，我有一个问题想要问你呢。”cl的脸有点红了起来。“嗯……好吧。问、问吧……我会告诉你的哦……”“那好。对于一个分数A / B……”“嗯……哎？哎？！”“……就是这个问题。我觉得这个问题好纠结啊……”Vani淡定地说完这句话。“啊？！哈啊？！”对于给定的分数 A / B，求其在 K 进制下是有限小数还是循环小数。如果是有限小数，求小数点后的位数；如果是循环小数，则求混循环部分和循环节的长度又分别是多少。 注意，循环节指的是最短循环节，且混循环部分的长度也指最短。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
Input
第一行一个正整数 T，表示测试数据的数目。

每个测试数据包含三个空格分隔的整数 A, B, K。含义如题目所示。

Output
对于每个测试数据，在单独的一行内输出两个空格分隔的整数 M, R。

其中 M 表示混循环部分的长度，R 表示循环节的长度。

如果 A / B 在 K 进制下是有限小数，则 R = 0，M 为小数点后面的位数；如果 A / B 在 K 进制下是纯循环小数，则 M = 0。

Sample Input
3

1 8 10

17 99 10

217 990 10

Sample Output
3 0

0 2

1 2

Data Constraint
对于 50% 的数据，B≤100000。

对于 100% 的数据，1≤A<B≤10^12，K≤10^12，T≤10。

准备学习基础数论。

T4 黑魔法师之门

Description

applepi被囚禁的地点只有一扇门，当地人称它为“黑魔法师之门”。这扇门上画着一张无向无权图，而打开这扇门的密码就是图中每个点的度数大于零且都是偶数的子图的个数对1000000009取模的值。此处子图 (V, E) 定义为：点集V和边集E都是原图的任意子集，其中E中的边的端点都在V中。 但是Vani认为这样的密码过于简单，因此门上的图是动态的。起初图中只有N个顶点而没有边。Vani建造的门控系统共操作M次，每次往图中添加一条边。你必须在每次操作后都填写正确的密码，才能够打开黑魔法师的牢狱，去拯救伟大的领袖applepi。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
Input
第一行包含两个整数N和M。

接下来M行，每行两个整数A和B，代表门控系统添加了一条无向边 (A, B)。

Output
输出一共M行，表示每次操作后的密码。

Sample Input
4 8

3 1

3 2

2 1

2 1

1 3

1 4

2 4

2 3

Sample Output
0

0

1

3

7

7

15

31

样例解释：

第三次添加之后，存在一个满足条件的子图 {1, 2, 3}（其中1, 2, 3是数据中边的标号）。

第四次添加之后，存在三个子图 {1, 2, 3}，{1, 2, 4}，{3, 4}。

子图不一定连通。举另外一个例子，例如点(1、2、3)，(4、5、6)分别组成一个三元环，则图中有三个所求子图。

 

Data Constraint
对于30% 的数据，N, M≤10。

对于100% 的数据，N≤200000，M≤300000。

一开始看到度数真的以为跟欧拉有什么关系,不过仔细一看不过就是一个判断环的问题。如果狂弄DFS我就无f**k说了。

再看一下数据,很大。如何找出答案的规律?

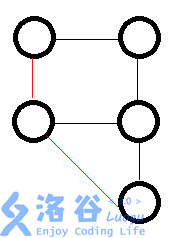
我们会发现上面的图每一次连,ans:=ans*2+1,也就是inc(ans,ans+1);

然后并查集维护一下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
//Title:黑魔法师之门

var
        fa:array[1..510000] of int64;
        n,m,l,r,fa1,fa2:int64;
        i:longint;
        ans:int64;

function get(x:longint):longint;
begin
        if fa[x]=x then
                exit(x)
        else
        begin
                get:=get(fa[x]);
                fa[x]:=get;
        end;
end;

begin
        read(n,m);
        for i:=1 to n do
                fa[i]:=i;
        ans:=0;
        for i:=1 to m do
        begin
                read(l,r);
                fa1:=get(l);
                fa2:=get(r);
                if fa1=fa2 then
                                begin
                        inc(ans,ans+1);
                                                ans:=ans mod 1000000009;
                                end
                else
                        fa[fa1]:=fa2;

                writeln(ans mod 1000000009);
        end;
end.

7.15 排名:19/32

T1 石子游戏

Description

Alice 和 Bob 总喜欢聚在一起玩游戏（T_T），今天他（她）们玩的是一款新型的取石子游戏。游戏一开始有N堆石子，Alice 和 Bob 轮流取出石子。在每次操作中，游戏者必须选择其中的一堆石子，并作出下列的其中一种操作： (1)移去整堆石子 (2)假设石子堆中有X颗石子，取出Y颗石子，其中1<=Y 游戏结束的条件是：取出最后一颗石子的人胜出。众所周知，Alice和Bob都是绝顶聪明的，假设他们在游戏中都采取最优的策略，问最后谁会胜出游戏呢？ Alice先取。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
Input

    第一行包含一个整数T，表示测试数据的组数。
    接下来T组测试数据，在每组数据中，第一行包含一个整数N，表示有多少堆石子。第二行N个正整数，分别表示每堆有多少颗石子。

Output

    每组测试数据输出一行，表示获胜者的名字（Alice 或者 Bob）。

Sample Input

3
3
3 5 6
4
2 3 6 9
5
3 2 1 1000000 999999

Sample Output

Alice
Bob
Alice

Data Constraint

20%的数据，N<=5，每堆石子数量少于10
100%的数据，T<=100，N<=100，每堆石子数量不大于1,000,000

SG函数了解一下:(预处理)

1
2
如果i是质数,那么SG[i]=离i最近的并且比i小的一个质数
如果i是合数,那么SG[i]=i的最小质因子

把每一个num[i] SG一下,然后对其进行Nimm博弈的xor就可以了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
var
        test,i,n,num,ans,tail:longint;
        shydog:array[1..1000002] of longint;
        judge:array[1..1000002] of longint;
        number:array[1..1000002] of longint;

procedure pretreatment;
var
        i,j:longint;
begin
        tail:=0;
        judge[1]:=1;
        shydog[1]:=1;
        for i:=2 to 1000001 do
        begin
                if judge[i]=0 then
                begin
                        inc(tail);
                        shydog[i]:=tail+1;
                        number[tail]:=i;
                end;
                for j:=1 to tail do
                begin
                        if i*number[j]>1000001 then
                                break;
                        judge[i*number[j]]:=number[j];
                        if i*number[j]=0 then
                                break;
                end;
        end;
        for i:=2 to 1000001 do
          if judge[i]>0 then shydog[i]:=shydog[judge[i]]; 
end;

begin
                Pretreatment;
                read(test);
                while test>0 do
                begin
                        read(n);
                        read(ans);
                        ans:=shydog[ans];
                        for i:=2 to n do
                        begin
                                read(num);
                                num:=shydog[num];
                                ans:=ans xor num;
                        end;
                        if ans=0 then
                                writeln('Bob')
                        else
                                writeln('Alice');
                        dec(test);
                end;
end.

T2 找回密码

Description

Kevin是一个热爱字符串的小孩。有一天，他把自己的微信登录密码给忘记了，万般无奈之下只好点“找回密码”。 这时候，网页上出现了当初设定的密保问题：在字符串st中，有若干个内容不同的子串，请问其中字典序第k小的子串是什么？ 很可惜的是，Kevin现在已经不会写程序了，所以，他找到了睿智的你来帮忙。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
Input

输入数据包括两行：第一行为字符串st，第二行为正整数k，定义如题目描述。
其中字符串st的长度不超过100,000且只由大小写英文字母组成

Output

一行，为第k小的字符串，如果字符串st中不足k个不同的子串，则输出字典序最大的一个。

Sample Input

AAB
2

Sample Output

AA

Data Constraint

50%的数据，|st| <=1000
100%的数据，|st|<=100,000，K < 2^63

后缀自动机是正解,正在学习中。

T3

Description

古老的汉诺塔问题是这样的:用最少的步数将N个半径互不相等的圆盘从1号柱利用2号柱全部移动到3号柱，在移动的过程中小盘要始终在大盘的上面。 　　现在再加上一个条件：不允许直接把盘从1号柱移动到3号柱，也不允许直接把盘从3号柱移动到1号柱。 　　把盘按半径从小到大用1到N编号。每种状态用N个整数表示，第i个整数表示i号盘所在的柱的编号。则N=2时的移动方案为： 　　(1,1)=>(2,1)=>(3,1)=>(3,2)=>(2,2)=>(1,2)=>(1,3)=>(2,3)=>(3,3) 　　初始状态为第0步，编程求在某步数时的状态。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
Input

　　输入文件的第一行为整数T(1<=T<=50000)，表示输入数据的组数。
　　接下来T行，每行有两个整数N,M(1<=n<=19,0<=M<=移动N个圆盘所需的步数)。

Output

　　输出文件有T行。
　　对于每组输入数据，输出N个整数表示移动N个盘在M步时的状态，每两个数之间用一个空格隔开，行首和行末不要有多余的空格。

Sample Input

4
2 0
2 5
3 0
3 1

Sample Output

1 1
1 2
1 1 1
2 1 1

可以找规律!!!!对不起,我是正统的递归:

真的想知道怎么做建议转看博客。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
var
        k,ans:array[0..100] of int64;
        test,m,n:int64;
        i:longint;

procedure move(x,y,a,b,c:int64);
begin
        if x=0 then
                exit;

        if y<=k[x-1] then
        begin
                ans[x]:=a;
                move(x-1,y,a,b,c);
                exit;
        end;
        if y<=k[x-1]*2+1 then
        begin
                ans[x]:=b;
                move(x-1,y-(k[x-1]+1),c,b,a);
                exit;
        end;

        ans[x]:=c;
        move(x-1,y-(k[x-1]*2+2),a,b,c);
end;

begin
        fillchar(k,sizeof(k),0);
        k[0]:=0;
        for i:=1 to 19 do
                k[i]:=k[i-1]*3+2;

        read(test);
        while test<>0 do
        begin
                read(n,m);
                fillchar(ans,sizeof(ans),0);
                move(n,m,1,2,3);
                for i:=1 to n do
                        write(ans[i],' ');
                writeln;
                dec(test);
        end;
end.

T4 城市统计

Description

中山(heihei)市的地图是一个n*n的矩阵，其中标号为1的表示商业区，标号为0的表示居民区。为了考察市内居民区与商业区的距离，并对此作出评估，市长希望你能够编写一个程序完成这一任务。 　　居民区i到商业区的距离指的是到距离它最近的商业区j的距离(|Xi-Xj|+|Yi-Yj|)，而你将统计的是对于城市中的每一个区域k，以它为中心，所有满足max(|Xk-Xm|,|Yk-Ym|)<=r的区域m到商业区距离之和。结果同样以n*n的矩阵形式输出。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
Sample Input

Sample Input1：
1
4 1
1 0 0 0
1 1 0 0
0 1 1 0
0 1 0 0

Sample Input2：
2
10 4
1 0 0 0 0 0 0 0 0 1
0 1 0 0 0 0 0 0 1 0
0 0 1 0 0 0 0 1 0 0
0 0 0 1 0 0 1 0 0 0
0 0 0 0 1 1 0 0 0 0
0 0 0 0 1 1 0 0 0 0
0 0 0 1 0 0 1 0 0 0
0 0 1 0 0 0 0 1 0 0
0 1 0 0 0 0 0 0 1 0
1 0 0 0 0 0 0 0 0 1

10 9
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1

Sample Output

Sample Output1：
1 4 9 8
2 5 10 9
2 4 7 7
2 3 4 4

Sample Output2：
40 50 57 63 70 70 63 57 50 40 
50 60 68 76 86 86 76 68 60 50 
57 68 76 85 97 97 85 76 68 57 
63 76 85 94 107 107 94 85 76 63 
70 86 97 107 120 120 107 97 86 70 
70 86 97 107 120 120 107 97 86 70 
63 76 85 94 107 107 94 85 76 63 
57 68 76 85 97 97 85 76 68 57 
50 60 68 76 86 86 76 68 60 50 
40 50 57 63 70 70 63 57 50 40 

0 0 0 0 0 0 0 0 0 0 
0 0 0 0 0 0 0 0 0 0 
0 0 0 0 0 0 0 0 0 0 
0 0 0 0 0 0 0 0 0 0 
0 0 0 0 0 0 0 0 0 0 
0 0 0 0 0 0 0 0 0 0 
0 0 0 0 0 0 0 0 0 0 
0 0 0 0 0 0 0 0 0 0 
0 0 0 0 0 0 0 0 0 0 
0 0 0 0 0 0 0 0 0 0

考试的时候没有想到题意,这里解释一下:我们对每一个居住区向每一个商业区建立最短距离,然后每一个点把在半径为r的正方形离的所有“距离”加起来。然后我打出来才20分。

这不是水题吗? 对不起,你现在想的70%不是正解。可乐的是,你所想的还有70分。

首先我们对每一个居住区建立一个值 way 代表它离商业区一带的最短距离,这个用Bfs就可以完成。接着,我们就可以暴力求出每一个点的ans,输出答案。

看来数据应该是卡了 r ,故意使r变得很大,那么我们怎么办?
建立二维前缀和。

首先我们把第1行,1列全部一维前缀和一遍,如图:

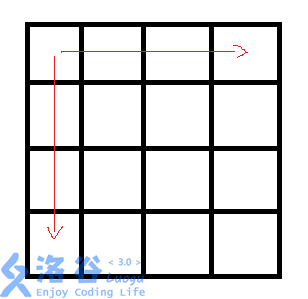
我们用 Ans[1,i]和ans[I,1]来标记一下,前缀和的变量是 way ([i,j])
然后我们建立二维前缀和 ans[i,j]:假如我们在3,3这个点,那么我们就减去上面那1个(注意不是r个),左边那1个,然后加上右上角那一个,记得加上自己的way。

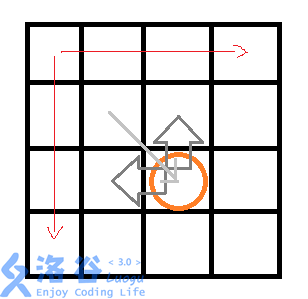
建完这张图后,我们就可以知道如何求出答案,如下图:

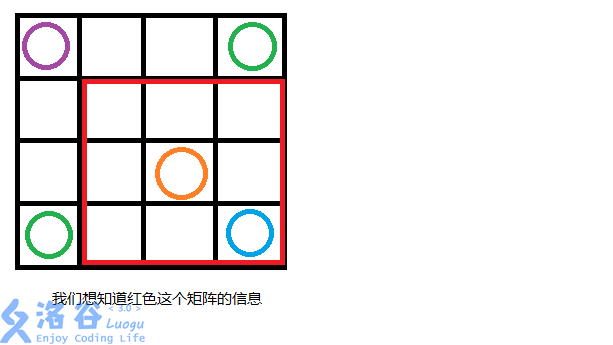
想知道(以橙色圆维中心)红色矩阵的信息,我们就用蓝色的圆减去绿色的圆加上紫色的圆的信息,注意运算的变量是 你建造的前缀和 ans。

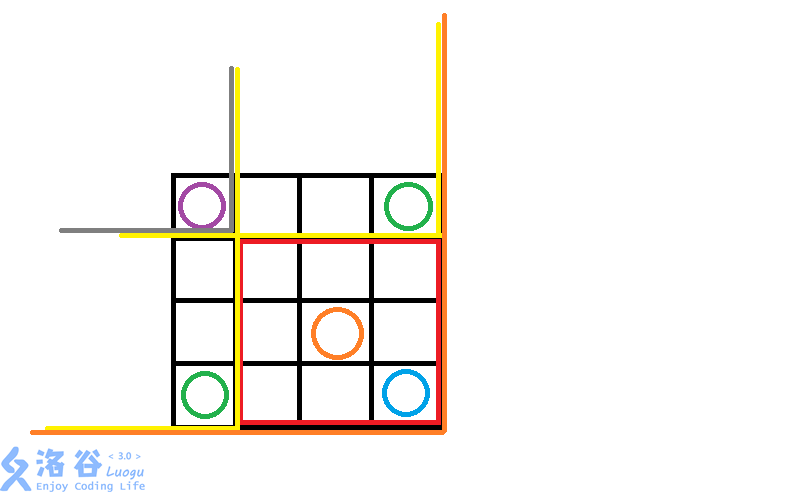
蓝色的圆的统领范围是橙色的边,绿色的点的统领范围是黄色的边,紫色的统领范围是灰色的边,相信聪明的你已经知道怎么做了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
Uses math;

var
        test:longint;
        dix:array[1..4,1..2] of longint;
        i,j,n,r,head,tail,x,y,x1,y1,sta,r1,r2,r3,r4:longint;
        queue:array[1..32255,1..2] of longint;
        ask:array[-160..320,-160..320] of shortint;
        way:array[-160..320,-160..320] of longint;
        ans:array[-160..320,-160..320] of longint;

procedure work;
begin
                fillchar(ask,sizeof(ask),0);
                fillchar(way,sizeof(way),0);
                head:=0;
                tail:=0;
                read(n,r);
                for i:=1 to n do
                        for j:=1 to n do
                        begin
                                read(sta);
                                if sta=1 then
                                begin
                                        inc(tail);
                                        queue[tail,1]:=i;
                                        queue[tail,2]:=j;
                                        ask[i,j]:=1;
                                end;
                        end;

                repeat
                        inc(head);
                        x:=queue[head,1];
                        y:=queue[head,2];
                        for j:=1 to 4 do
                        begin
                                x1:=x+dix[j,1];
                                y1:=y+dix[j,2];
                                if (x1>0)and(y1>0)and(x1<n+1)and(y1<n+1)and(ask[x1,y1]<>1) then
                                begin
                                        ask[x1,y1]:=1;
                                        way[x1,y1]:=way[x,y]+1;
                                        inc(tail);
                                        queue[tail,1]:=x1;
                                        queue[tail,2]:=y1;
                                end;
                        end;
                until head>=tail;

                for i:=1 to n do
                        ans[i,1]:=ans[i-1,1]+way[i,1];
                for i:=1 to n do
                        ans[1,i]:=ans[1,i-1]+way[1,i];
                for i:=1 to n do
                        for j:=1 to n do
                                ans[i,j]:=ans[i-1,j]+ans[i,j-1]-ans[i-1,j-1]+way[i,j];
                for i:=1 to n do
                begin
                        for j:=1 to n do
                        begin
                                r1:=max(i-r,1);
                                r2:=max(j-r,1);
                                r3:=min(i+r,n);
                                r4:=min(j+r,n);
                                write(ans[r3,r4]-ans[r3,r2-1]-ans[r1-1,r4]+ans[r1-1,r2-1],' ');
                        end;
                        writeln;
                end;
                writeln;
end;

begin
                dix[1,1]:=1;
                dix[2,2]:=1;
                dix[3,1]:=-1;
                dix[4,2]:=-1;

                read(test);
                while test>0 do
                begin
                        work;
                        dec(test);
                end;
end.

好了,JZOI的生活到此并没有告终,下一个月还有一期,敬请期待!