后缀数组排序浅谈
后缀排序服务后缀数组,可以解决众多的字符串问题,如:后缀的最大公共前缀、可重叠最长重复子串、不可重叠最长重复子串、本质不同的子串的数量(参考自自为风月马前卒)。这里就来讲一下如何对后缀数组进行排序。
基础知识
I.后缀、后缀数组(Suffix array)
本质就是i(1<=i<=len(S))以后的字符串G(G是字符串S的子串),那么G就是S的后缀。举一个例子,aabbc的后缀有这些:1
2
3
4
51.a
2.aa
3.aab
4.aabb
5.aabbc (注意是包括它自己的)
那么顾名思义,后缀数组就是存储字符串S的后缀的数组。
II.枚举排序方法
1.可以用各种普通的数字排序法,比如基数排序,快速排序,堆排序等等…
2.运用倍增排序法(Double Algorithm),时间复杂度为O(n log n)。
3.运用CD3(三分算法、Difference Cover moudlo 3),官方认为是O(n*k),其中k为一个未知而可怕的常数。个人认为是O(n+2/3n log 2/3n)。(n代表的是字符串S的后缀个数)
讲解并分析以上排序方法
I类.暴力排序 (n+n log n^2) -> (n+n^2)
什么,暴力?O(len log len)还想怎么样?那你就大错特错了,因为2个字符串比较是需要len的时间的,所以快速排序等O(n log n)的排序就会变为:O(len log len^2)。而一开始需要提取后缀,只需弄一个前缀和就可以了,所以是len。
当然,如果使用基数排序是可以达到len^2,详见My Luogu 博客?所以对于数字的排序运用到字符串上面,吃亏不小。
II类.倍增排序 (n log n)
这种排序甚至连后缀都不用提取,因为它直接把序号存储到一个数组里面。排完序的数组a[i]就是代表以i为起点的后缀在字符串S中的字典序排名。
那么我们如何排序,按照步骤来说:
我们先把原本的每一个字符全部按照字典序给一个编号,编号数组为num[i]。然后创建一个存储2^k的数组log,log[0]=1,log[10]=1024 (log[k]=2^k)。其次我们把num[i]和num[log[j]+i-1]合并为num[i],其中j就是我们现在已经排序了几次,举一个上面的例子:1
aabaab -> 编号数组num [1,1,2,1,1,2] , 合并,j=1,log[j]=2。
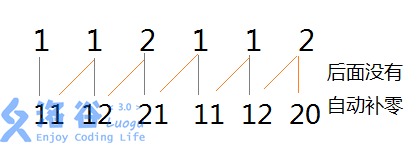
然后我们对合并后的数组进行再一次排序:
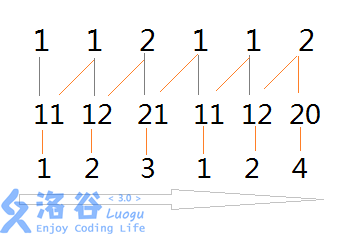
然后继续合并,注意j已经是2了:
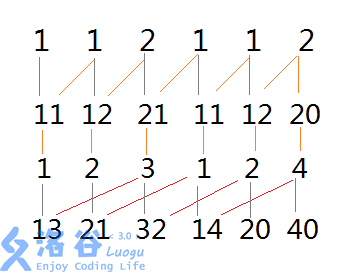
宏观图片就是:
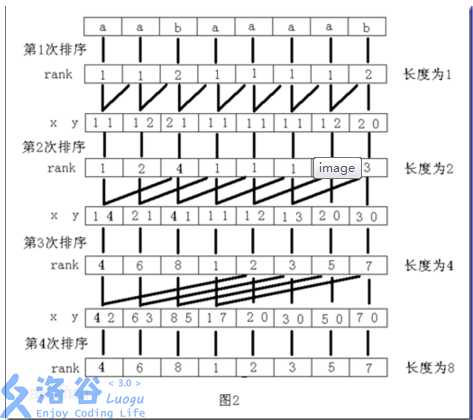
边界问题,应该是log n次吧。最后的num数组就是排完序的了。然后平时单、双、多字符是可以用基数排序的吧。
III类.CD3 3分算法排序 (1/3n log 1/3n+n+2/3n log 2/3n) / (n)
其实很简单,就是把i mod 3=0的后缀全部取出来,不参与排序。然后对那些i mod 3<>0的后缀进行倍增排序,最后把i mod 3=0的后缀合并一下(归并排序,注意只有两个都是有序的,才能强制线性归并)。
这种方法真的是SAO,代码复杂度也是很强。不过理论复杂度要好很多吧。(注意常数问题)
参考博客、PPT
II 自为风月马前卒
IV PPT