浅谈分块思想

一种用于区间的比高难的线段树好懂线性数据结构。不要看我写了怎么多,其实只是细节罢了,很适合新手学习。

什么是”分”,什么是”块”?

分,顾名思义,就是把一个区间分成很多个部分。块,顾名思义,就是一块一块的区间。那我们为什么要把区间分成块呢?

想想普通的线段树,其实就是把一些区间变成整体。分块也正是这样,它把n个数分成了trunc(sqrt(n)) (注意是向下取整)。如图:

(声明,以下的trunc(sqrt(n)) 被写为 q(n))

我们为什么要分成 trunc(sqet(n)) 多块?因为可以均摊复杂度。(看过斐波那契堆的都应该知道)

我们要想清楚的几个细节,块数和每一个块里面有多少个数一样吗?我们的分块从1还是0开始?回答:不一样,块数(k)如果刚好开方n那么k=q(n)否则就是k=q(n)+1,而块数(kk)不管有没有数(因为有不开方的情况)始终保持kk=q(n)。我们可以随便从1或0开始,但是以下的讲解均从1开始。

从1开始又有细节(都是从血史中提取的!!),如果kk=4(k=4,n=10),node=5那么应该在第二块。所以我们有一个点node,我们不能直接用 node div kk ,也不可以 node div kk+1 来求它在哪一块。如果 node 不可以整除 kk,那么我们需要给它+1。做几道练习:

1
2
3
4
5
6
function make(n:longint):longint; //看n在哪一块,n指的是node而不是数的个数
 begin     
        if (n mod kk=0) then //以下依据上述       
            exit(n div kk);     
        exit(n div kk+1); 
end;
1
2
1.kk=30,k=30,n=901 符合实际吗?
2.当kk=101,node=202的时候,node在第几块?

Answer:

1
2
1.不符合,因为n不能被整开方,所以应该是k=31(注意kk是没有错的)
2.1到101是第一块,102到202是第二块,203到303是第三块....,第二块。

那么我们又有什么操作呢?

区间操作

如果你还不知道线段树的单点操作,请先学习线段树,这里直接上区间操作。

区间修改

我们要修改区间l,r的时候,我们就可以在l,r的区间内的”块”(注意这里的块指的是区间内最大的块)进行q(n)复杂度的修改操作。也就是说,我们可以定义数组 interadd 称为整体要加值,每一次整块加入值的时候,我们就可以改变 interadd 的值。一般是 inc(interadd[i],add)。那区间内有kk个数,每一个都要加add,不是kk乘add吗,我说的是整体要加,所以就加add就可以了,我们就潦草的敷衍了整个区间。聪明的肯定就知道区间查询的时候要做什么。

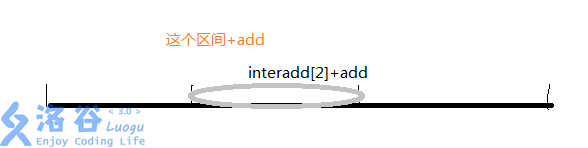
那么我们怎么求中间的大块很知道旁边出界的区域呢?其实很简单,上面已经讲了怎么求哪个点在哪一块,我们先 (real代表所在的最大块的最左和最右两个块)
real[1]:=make(l),real[2]:=make(r)就可以直接得出l和r所在的块。但是还要注意,中间的块是real[1]+1到real[2]-1。

1
2
for i:=real[1]+1 to real[2]-1 do  //注意real数组代表的是块的编号的左右,
    inc(interadd[i],add); //整体+add

我们有一个问题,如果l,r出界了怎么办？
简单!暴力!我们把左边出界的和右边出界的全部暴力加add就可以了!这里就要引入数组 num 就是代表一个点(注意不是一个块)共有的值是多少。

1
2
3
4
5
6
7
8
9
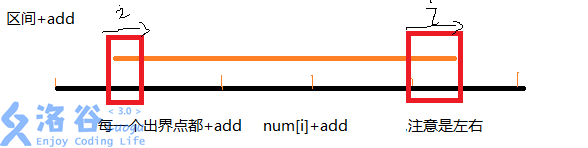
10
for i:=l to real[1]*kk do //注意注意! real[1]是块那么转化成点就应该是real[1]*kk     
begin             
    inc(num[i],add); //个人加
    inc(intersum[real[1]],add); //个人加了,那么整体也加了,intersum不是interadd,它的定义是整体 num 的值   
end;         
for i:=(real[2]-1)*kk+1 to r do //大佬推出来的 (real[2]-1)*kk+1 真是太强了!! 
begin             
    inc(num[i],add); //个人加            
    inc(intersum[real[2]],add); //整体加         
end;

问一个问题,如果2<=n<=100000,那么intersum 或 interadd 要开多少个数?这不是废话,q(n)。

我们剩下最后一种情况,real[1]=real[2],意思是l和r在同一个区间。我们不确定l,r是不是这个区间的左右,有可能在里面,所以就需要暴力!

1
2
3
4
5
for i:=l to r do         
begin             
	inc(num[i],add);             
   	inc(intersum[real[1]],add); //注意intersum,所以是real[1]而不是i (make(i)或者是real(2)是没有所谓的)         
end;

区间查询

区间查询与修改极其类似,大同小异罢了。

一开始我们 find 的值肯定是0,然后再求出real[1]和real[2]就可以了。再像修改一样,我们判断两种情况:1.real[1]和real[2]不在同一个块上面,2.在同一个块上面。

在同一个块,暴力!注意判断的时候:

1
2
3
4
5
if real[2]-real[1]<=1 then   
begin         
    for i:=l to r do         
        inc(find,num[i]+interadd[make(i)]);  //就是说整体加了多少和个人本来的值和个人加了多少=这个地方加了多少。那为什么 interadd[make(i)]要make(i)呢?因为它是每一个 区间 每一个点 加了多少诶。 
end

然后就是不同一个块：

1
2
3
4
5
6
for i:=real[1]+1 to real[2]-1 do //记住是l的分块+1到r的分块-1             
    inc(find,intersum[i]+kk*interadd[i]); //为什么变成了整体的值+整体加了多少,而上面不是?因为上面是点啊,这里整体的值已经包括点了,但是我们需要减少时间复杂度就这样做啊。interadd[i]为什么要乘上kk?这个就是定义的问题了啊。     
for i:=l to real[1]*kk do             
    inc(find,num[i]+interadd[real[1]]); //注意出界是一个一个点的加        
for i:=(real[2]-1)*kk+1 to r do             
    inc(find,num[i]+interadd[real[2]]); //同上

个人认为已经非常详细,大家读完以后一定要注意分块的细节。我也是在打题解的时候弄懂了很多东西,欢迎大家吐槽或有疑问(最好是私信)。代码的话可以借鉴别人C++的,可以看出我是打pascal的,而且比较丑。准备下次再发。

Code:

一个钟头后的代码补救。注意有一些地方是不一样的,所以仅供参考。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
// luogu-judger-enable-o2

Uses math;
var
    block_num,node_num,mode,i,n,m,x,y:longint;
    find,add:int64;
    intersum,interadd:array[-1..500] of int64;
    num:array[-1..100100] of int64;

function Locate(node:longint):longint;
begin
    if node mod node_num=0 then
        exit(node div node_num);
    exit(node div node_num+1);
end;

procedure Change(l,r:longint;add:int64);
var
    i:longint;
    real:array[1..2] of longint;
begin
    real[1]:=Locate(l);
    real[2]:=Locate(r);
    if real[1]=real[2] then
    for i:=l to r do
    begin
        inc(num[i],add);
        inc(intersum[real[1]],add);
    end
    else
    begin
        for i:=real[1]+1 to real[2]-1 do
            inc(interadd[i],add);
        for i:=l to real[1]*node_num do
        begin	
            inc(num[i],add);
            inc(intersum[real[1]],add);
        end;
        for i:=(real[2]-1)*node_num+1 to r do
        begin
            inc(num[i],add);
            inc(intersum[real[2]],add);
        end;
    end;
end;

procedure Query(l,r:longint);
var
    i:longint;
    real:array[1..2] of longint;
begin
    find:=0;
    real[1]:=Locate(l);
    real[2]:=Locate(r);
    if real[2]-real[1]<=1 then
        for i:=l to r do
            inc(find,num[i]+interadd[Locate(i)])
    else
    begin
        for i:=real[1]+1 to real[2]-1 do
            inc(find,intersum[i]+node_num*interadd[i]);
        for i:=l to real[1]*node_num do
            inc(find,num[i]+interadd[real[1]]);
        for i:=(real[2]-1)*node_num+1 to r do
            inc(find,num[i]+interadd[real[2]]);
    end;
end;

procedure Ready;
var
    i,j:longint;
begin
    read(n,m);
    node_num:=trunc(sqrt(n));
    block_num:=trunc(sqrt(n));
    if block_num<>sqrt(n) then
        inc(block_num);

    for i:=1 to n do
        read(num[i]);
    j:=1;
    for i:=1 to n do
    begin
        inc(intersum[j],num[i]);
        if i mod (block_num-1)=0 then
            inc(j);
    end;
end;

begin
    Ready;
    for i:=1 to m do
    begin
        read(mode,x,y);
        if mode=1 then
        begin
            read(add);
            Change(x,y,add);
        end
        else
        begin
            Query(x,y);
            writeln(find);
        end;
    end;
end.